
- #CONSTRUCTION OF AN ALTITUDE GEOMETRY HOW TO#
- #CONSTRUCTION OF AN ALTITUDE GEOMETRY FULL#
Students may need to sketch the final sample problem to recognize that it matches the image. Note that they could use the Pythagorean Theorem to solve all three problems, since that is where the labels on the image come from. Similarly, the diagonal of a square divides it in half to match that image. Students may recognize the height of an equilateral triangle divides it in half to match the image. When she looks up at the top of the building, she measures the angle from the ground to the top of the building to be \(60^\). An engineer is standing 10 meters away from a building.(iii) From point B, mark an arc taking 4 cm as radius. (ii) From point A, mark an arc taking 5 cm as radius. The diagonal of a square is \(5\sqrt2\) units. Solution: Following are the steps of construction of a parallelogram whose diagonals and one side is given: (i) Construct line segment AB of length 7 cm.The side length of an equilateral triangle is 8 units.Here are three sample problems to discuss: Ask students how they might decide what types of problems to use it on, and how they would solve those problems.
#CONSTRUCTION OF AN ALTITUDE GEOMETRY FULL#
If applicable, remind students that this type of image might be provided as a reference on standardized tests. Total Pageviews Here is a full proof formula to calculate net national income at factor cost. In comparison, a Boeing 747 averages about 540 mph at cruising altitude.
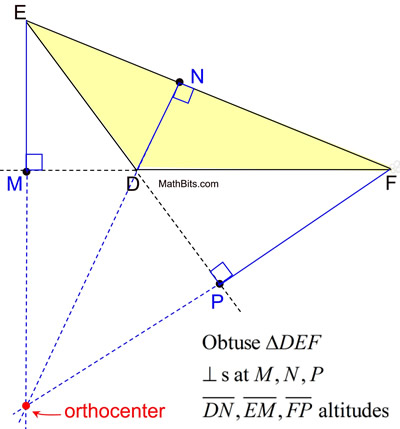
Why are we looking at two triangles? Are the triangles related? What are we going to do with these?) Build An Elevated Model Train TrackThe resulting model, measuring a tiny 1/8.

Ask students what they notice and what they wonder about the images.
A right triangle when one side is 3.5 cm and sum of other sides and the hypotenuse is 5.5 cm. A triangle PQR given that QR = 3cm, ∠PQR = 45° and QP - PR = 2 cm. #CONSTRUCTION OF AN ALTITUDE GEOMETRY HOW TO#
A triangle if its perimeter is 10.4 cm and two angles are 45° and 120°. In this tutorial students will learn how to construct an altitude of a triangle using a compass and a straight edge.If You Like It, Like ItIYLILIPlease clic. An equilateral triangle of altitude 6 cm is constructed above Give justification for your construction.Īn Equilateral triangle is a triangle in which all three sides are equal and angles are also equal. Prove: If an isosceles triangle has an altitude from the vertex to the base, then the altitude bisects the vertex angle. NCERT Exemplar Class 9 Maths Exercise 11.4 Sample Problem 1 Construct an equilateral triangle if its altitude is 6 cm. ☛ Also Check: NCERT Solutions for Class 9 Maths Chapter 11 Give justification for your construction. Find the length of the altitude from R to PQ. Construct a PQR in which PQ 8 cm, R 60° and the median RG from R to PQ is 5.8 cm. ✦ Try This: Construct an equilateral triangle if its altitude is 5 cm. Construction of a triangle when its base, the vertical angle and the median from the vertex of the base are given. Anytime you can construct an altitude that cuts your original triangle. Thus, an equilateral triangle with altitude 6 cm is constructed. The other leg of the right triangle is the altitude of the equilateral triangle, so solve using the Pythagorean Theorem: a2 + b2 c2 a 2 + b 2 c 2. ∆ABC is an equilateral triangle with AD of length 6 cm ∠A = 30° + 30° = 60° and AD is perpendicular to BC ∠CAD and ∠BAD where B and C lie on the line XYĥ. Generate 30° at A on both sides of AD, i.e. Now cut a line segment AD from D which is equal to 6 cmĤ. Construct a line XY and consider a point D on this lineģ. Give justification for your construction.ġ. 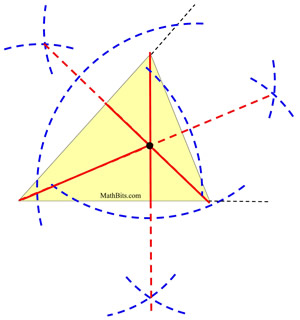
Construct an equilateral triangle if its altitude is 6 cm.







 0 kommentar(er)
0 kommentar(er)
